Relative survival

When describing the survival experience of a group of people or patients typically the method of overall survival is used, and it presents estimates of the proportion of people or patients alive at a certain point in time. The problem with measuring overall survival using Kaplan-Meier or actuarial survival methods, is that the estimates include two causes of death: 1) deaths due to the disease of interest and; 2) deaths due to all other causes, which includes old age, other cancers, trauma and any other possible cause of death. In general, we are interested in the deaths due to a disease rather than all causes, and therefore a "cause-specific survival analysis" is employed to measure disease-specific survival. Thus, there are two ways in performing a cause-specific survival analysis:

Competing Risks Survival Analysis - This form of analysis is known by its use of death certificates. In traditional overall survival analysis the cause of death is irrelevant to the analysis. In a competing risks survival analyses each death certificate is reviewed. If the disease of interest is cancer, and the person/patient dies of a car accident, the patient is labelled as censored at death, instead of being labelled as having died. Issues with this method arise as each hospital and or registry may code for causes of death differently. For example, there exists variability in the way a patient who has cancer and commits suicide is coded/labelled. In addition, if a patient has an eye removed due to an ocular cancer and dies getting hit while crossing the road because he didn't see the car would often be considered to be censored rather than having died due to the cancer or its subsequent effects.
Relative Survival - This form of analysis is more complex, but considered the gold-standard for performing a cause-specific survival analysis. It is based on two rates:

the overall hazard rate observed in a diseased population
the background or expected hazard rate in the general or background population.

Essentially, deaths due to the disease in a single time period equals the total number of deaths (overall number of deaths) minus the expected number of deaths in the general population. Therefore, if a population of cancer sufferers suffer 10 deaths per hundred population, but only 1 death occurs per hundred general population, then the disease specific number of deaths (excess hazard rate) equals 9 deaths per hundred population. The classic equation for the excess hazard rate is as follows:

$\lambda = \lambda^*%2B\nu\,\!$

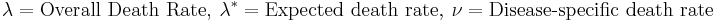
$\lambda = \text{Overall Death Rate},~\lambda^*=\text{Expected death rate},~\nu=\text{Disease-specific death rate}$

Note that this equation doesn't define a survival proportion, but simply describes the relationships between disease-specific death (excess hazard) rates, background mortality rates (expected death rate), and the overall observed mortality rates. The excess hazard rate is related to relative survival, just as hazard rates are related to overall survival.

Relative survival is typically used in the analysis of cancer registry data.^[1] Cause-specific survival estimation using the coding of death certificates has considerable inaccuracy and inconsistency, thus not permitting the comparison of rates across registries. This is because the diagnosis of cause-of-death is varied between practitioners. How does one code for a patient who dies of heart failure, after having received a chemotherapeutic agent which has known deleterious cardiac side-effects? In essence, it doesn't really matter why the population dies, what matters is if the rate of death is higher than that of the general population. So if all patients are all dying of car crashes, perhaps the tumor and/or treatment predisposes them to have visual and/or perceptual disturbances which lead them to be more likely to die in a car crash. In addition, it has been shown that patients coded in a large US cancer registry as suffering from a non-cancer death are 1.37 times as likely to die as a member of the general population.^[2] If the coding was accurate, this figure should approximate 1.0 as the rate of those dying of non-cancer deaths (in a population of cancer sufferers) should approximate that of the general population. Thus, the use of relative survival provides an accurate way to measure survival rates associated with the cancer in question.

In epidemiology, relative survival (as distinct from overall survival, and associated with excess hazard rates) is defined as the ratio of observed survival in a population to the expected or background survival rate.^[3] It can be thought of as the kaplan-meier survivor function for a particular year, divided by the expected survival rate in that particular year. This is typically known as the relative survival (RS). If 5 consecutive years are multiplied, the resulting figure would be known as cumulative relative survival (CRS). This is analogous to the 5-year overall survival rate, but it is a way of describing cancer-specific risk of death over 5 years after diagnosis.

There are several software suites available to estimate relative survival rates. Regression modelling can be performed using maximum likelihood estimation methods, using Stata or "R".^[4]^[5]

References

^ Gamel, JW (2001). "Non-parametric comparison of relative versus cause-specific survival in Surveillance, Epidemiology and End Results (SEER) programme breast cancer patients". Statistical Methods in Medical Research 10: 393-352.
^ Brown, BW (1993). "Noncancer deaths in white adult cancer patients.". Journal of the National Cancer Institute 85 (12): 979–987.
^ "Measures of Cancer Survival". http://surveillance.cancer.gov/survival/measures.html. Retrieved November 24, 2010.
^ Dickman PW, Sloggett A, Hills M, Hakulinen T. (2004). "Regression models for relative survival". Stat Med 23 (1): 51–64.
^ Lambert PC, Thompson JR, Weston CL, Dickman PW. (2007). "Estimating and modeling the cure fraction in population-based cancer survival analysis". Biostatistics 8 (3): 576–94.

Relative survival

See also

References